CLASS-8
CLASSIFICATION OF TRIANGLE ON BASICS OF SIDES

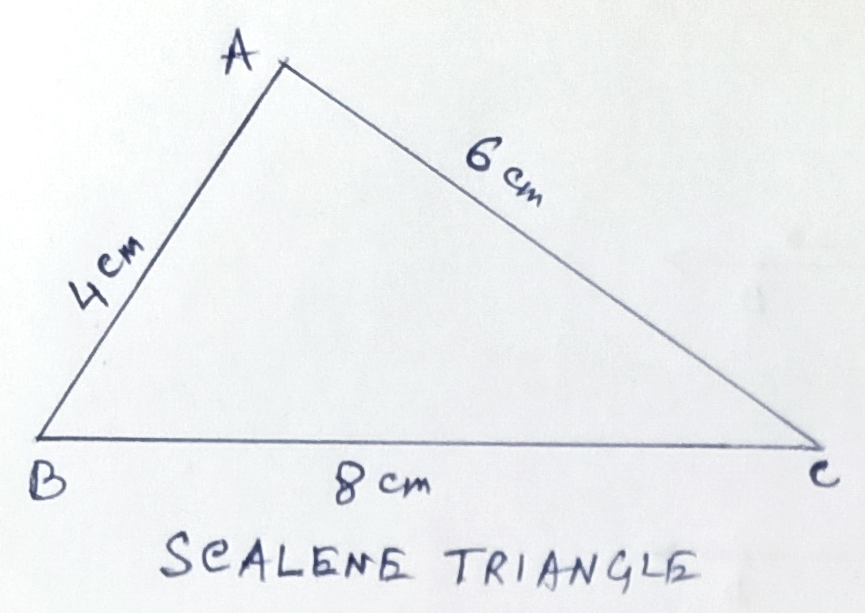
No two sides of a scalene triangle are equal. In the figure, ABC is a scalene triangle as AB ≠ BC ≠ CA

Isosceles Triangle –

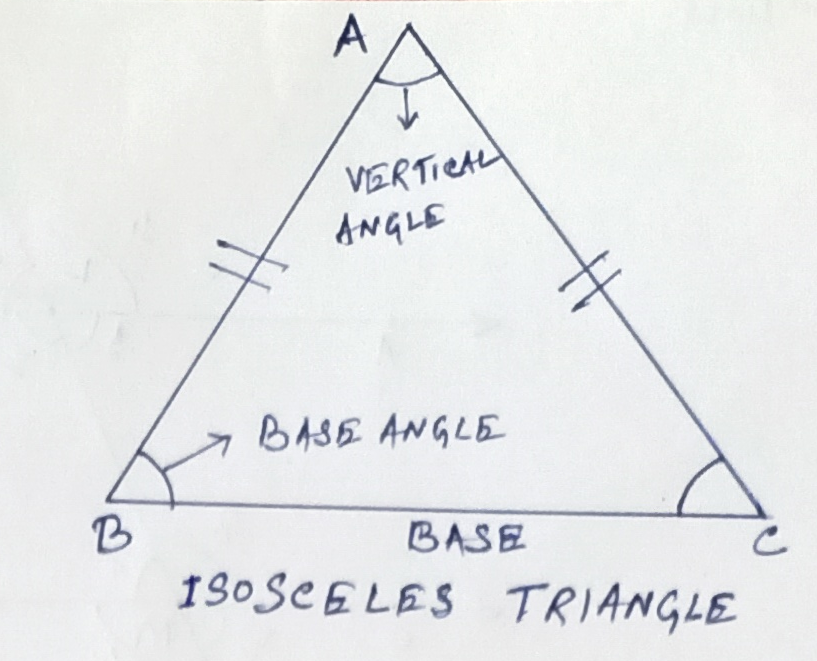
An Isosceles triangle has two equal sides. In the figure, ABC is an isosceles triangle in which AB = AC (equal sides are marked by an equal number of strokes). The third side BC is called the base of the triangle, while ∠ABC and ∠ACB are called the base angles. ∠BAC is called the vertical angle.

Property –

The angles opposite to the equal sides of an isosceles triangle are equal.

In the figure, AB = AC,

So, ∠ABC = ∠ACB

Converse –

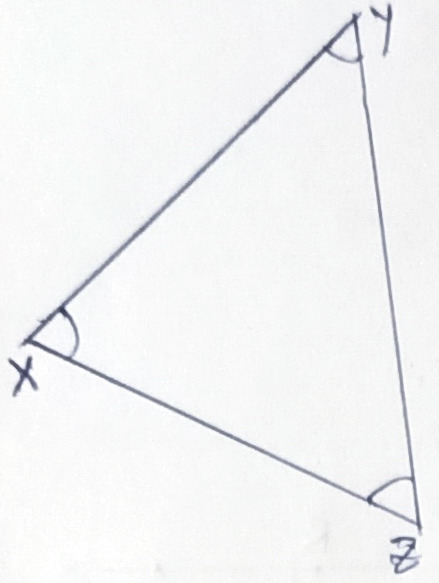
The converse, or opposite, of this is also true. Thus, if two angles of a triangle are equal, the sides opposite to them are equal.

In the figure, ∠ABC = ∠ACB.

So,  AB = AC

This also implies that the angles of a scalene triangle are all unequal.

Equilateral Triangle –

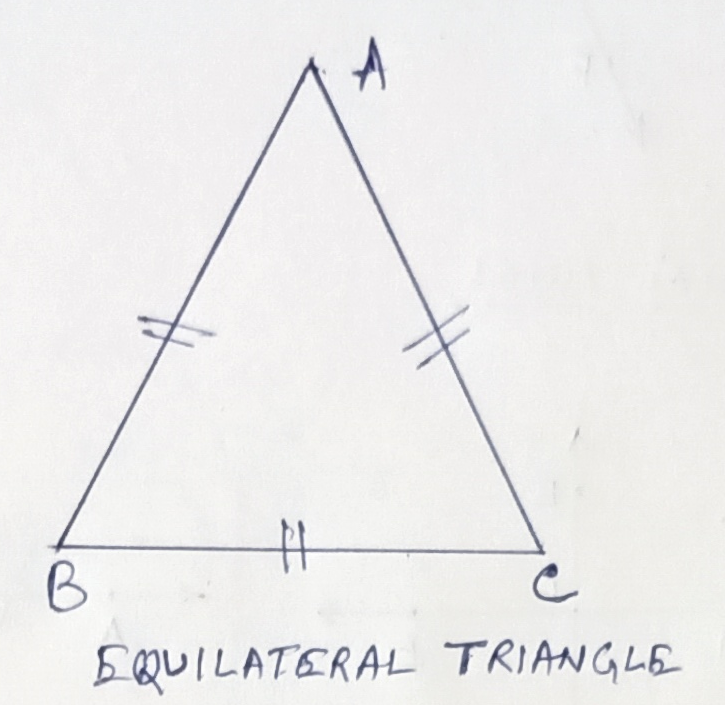
All the three sides of an equilateral triangle are equal. In the adjoining figure, ABC is an equilateral triangle as AB = BC = CA

Property –

All the angles of an equilateral triangle are equal.

In the figure, ∠BAC = ∠ABC = ∠ACB

Converse –

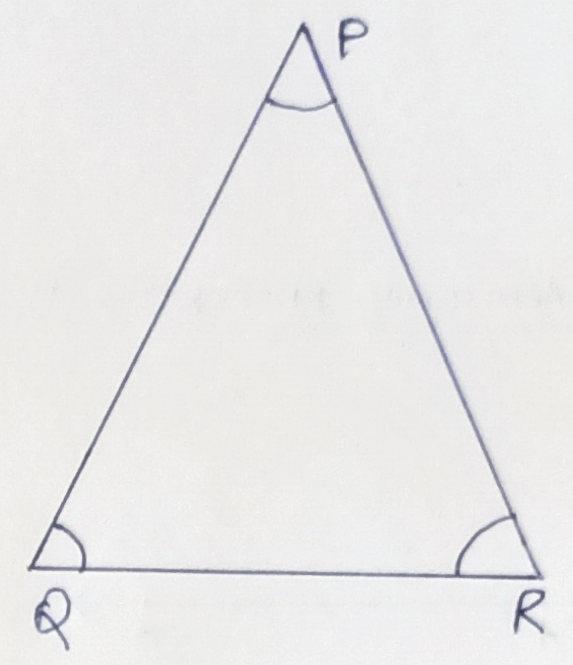
If all the angles of a triangle are equal, it must be an equilateral triangle.

In the adjoining figure, ∠P = ∠Q = ∠R,

Hence, PQR is an equilateral triangle.