CLASS-8
PYTHAGORAS THEOREM - PROBLEM & SOLUTION

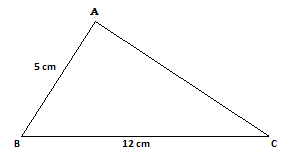
Ans.)  As per the Pythagoras theorem AC² = AB² + BC²

As per the above given picture AB = 5 cm and BC = 12 cm

So, AC² = 5² + 12² = 25 + 144 = 169

Or, AC  =  √169  = √13² =  13   (Ans.)

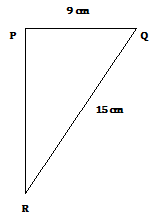
Ans.) As per the Pythagoras theorem  QR² = PQ² + RP²

As per the above given picture PQ = 9 cm and  QR = 15 cm

So,   15² =  9² + PR² 

Or,   PR² =  15²- 9²

Or,   PR² =  225 – 81 = 144

Or,   PR  =  √144  =  √12² =  12  (Ans.)

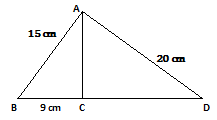
Ans.)  In ∆ ABC, AB² =  AC²+ BC², by Pythagoras theorem

Here from the above given picture we can find, AB = 15 cm, BC = 9 cm

So, AB² = AC² + BC²

Or,     15² =  AC² +  9²

Or,     225 = AC² + 81

Or,     AC² = 225 – 81 =  144

Or,     AC =  √144 =  √12² =  12 cm

Now, in ∆ ACD, AD² = AC² + CD², by Pythagoras theorem

Here we can find from the above given picture, AC = 12 cm, AD = 20 cm.

So,    AD² =  AC² + CD²

Or,    20² =  12² + CD²

Or,    400 = 144 + CD²

Or,    CD² =  400 – 144 = 256

Or,     CD = √256 =  √16² = 16 cm

Now,   BD = BC + CD

Or,         = 9 + 16 = 25

We can observe that, BD² = AB² + AD² 

                              = 15² + 20² = 225 + 400 = 625

                          BD =  √625 =  √25²  =  25

In, ∆ ABD is a right angled triangle in which BD is the hypotenuse, that is, √A = 90⁰            (Ans.)

Example.3) Find PQ in the following figure.

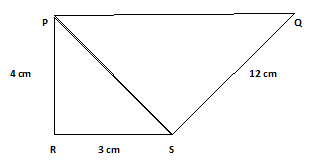
Ans.)  In the right angled ∆ PRS, PS² = PR² + RS², from the above given picture we can find  -

PR = 4 cm, and  RS = 3 cm     

Or,  PS² =  4² + 3²  =  16 + 9 = 25

Or,   PS  =  √25  =  √5²  =  5  cm            

In the right angled ∆ PRS, PQ² = PS² + SQ², from the above given picture we can find  -

         PS = 5 cm, and  SQ = 12 cm     

 Or,   PQ² =  5² + 12² =  25 + 144 =  169

Or,    PQ  =  √169 =  √13² =  13 cm          

So,  we can find that, PQ = 13 cm               (Ans.)

Example.4) Calculate ‘x’ in below figure

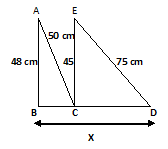
Ans.) In ∆ ABC, AC² = AB²+ BC², by Pythagoras theorem

 From above given picture, AB = 48 cm, and AC = 50 cm

So,  AC² =  AB² + BC²

Or,  50² = 48² + BC²

Or,  BC² = 50² - 48²

           = 2500 – 2304 = 196

Or,   BC² = 196

Or,   BC = √196 = √14² =  14

Now, in ∆ ECD,  ED² = EC²+ CD², by Pythagoras theorem

From the above given picture, ED = 75 cm, and EC = 45 cm

So,  ED² =  EC² + CD²

Or,   75² = 45² + CD²

Or,   5625 =  2025 + CD²

Or,   CD² = 5625 – 2025 =  3600

Or,   CD = √3600 = √60² = 60

Now, as we can find from the above picture, x = BC + CD

Here we find, BC = 14 cm, and CD = 60 cm.

Now,  x = BC + CD = 14 + 60 = 74 cm

So, the desired answer is 74 cm      (Ans.)