CLASS-8
PARALLELOGRAM- PROBLEM & SOLUTION
PROBLEM & SOLUTION
Example.1) In the figure ABCD is a parallelogram. Find x & y
Ans.) The opposite sides of a parallelogram are equal.
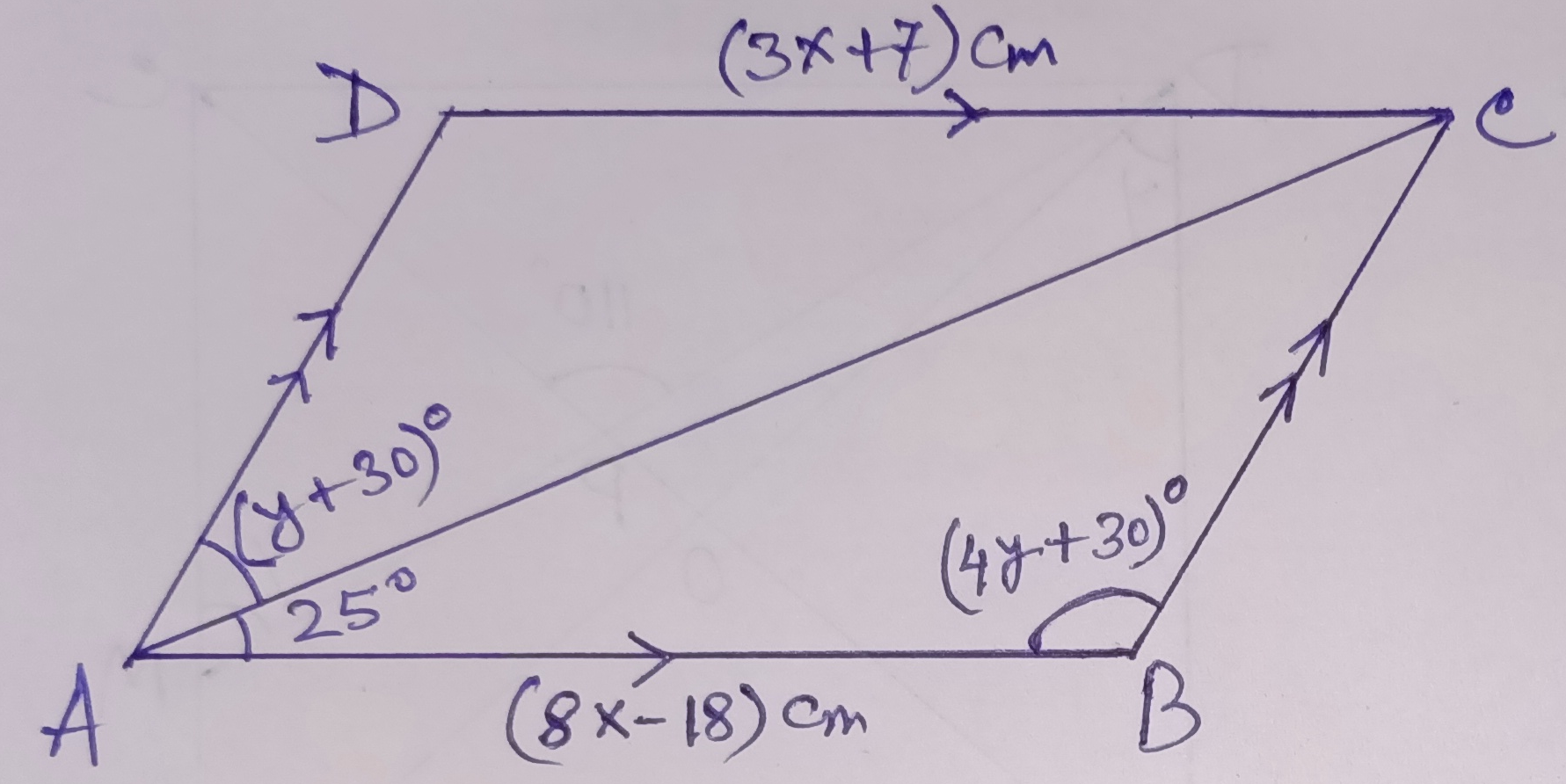
So, AB = DC
=> 8x – 18 = 3x + 7
=> 5x = 25
=> x = 5
So, AB = DC => ∠A + ∠B = 180⁰ as these are co-interior angles
=> y + 30 + 25 + 4y + 30 = 180
=> 5y = 180 – (30 + 30 + 25) = 95
=> y = 95/5 = 19
Hence we can get x = 5, and y = 19 (Ans.)
Example.2) In the adjoining figure, ABCD is a rectangle. Find x, y, & z
Ans.) The diagonals of a rectangle are equal and they bisect each other.
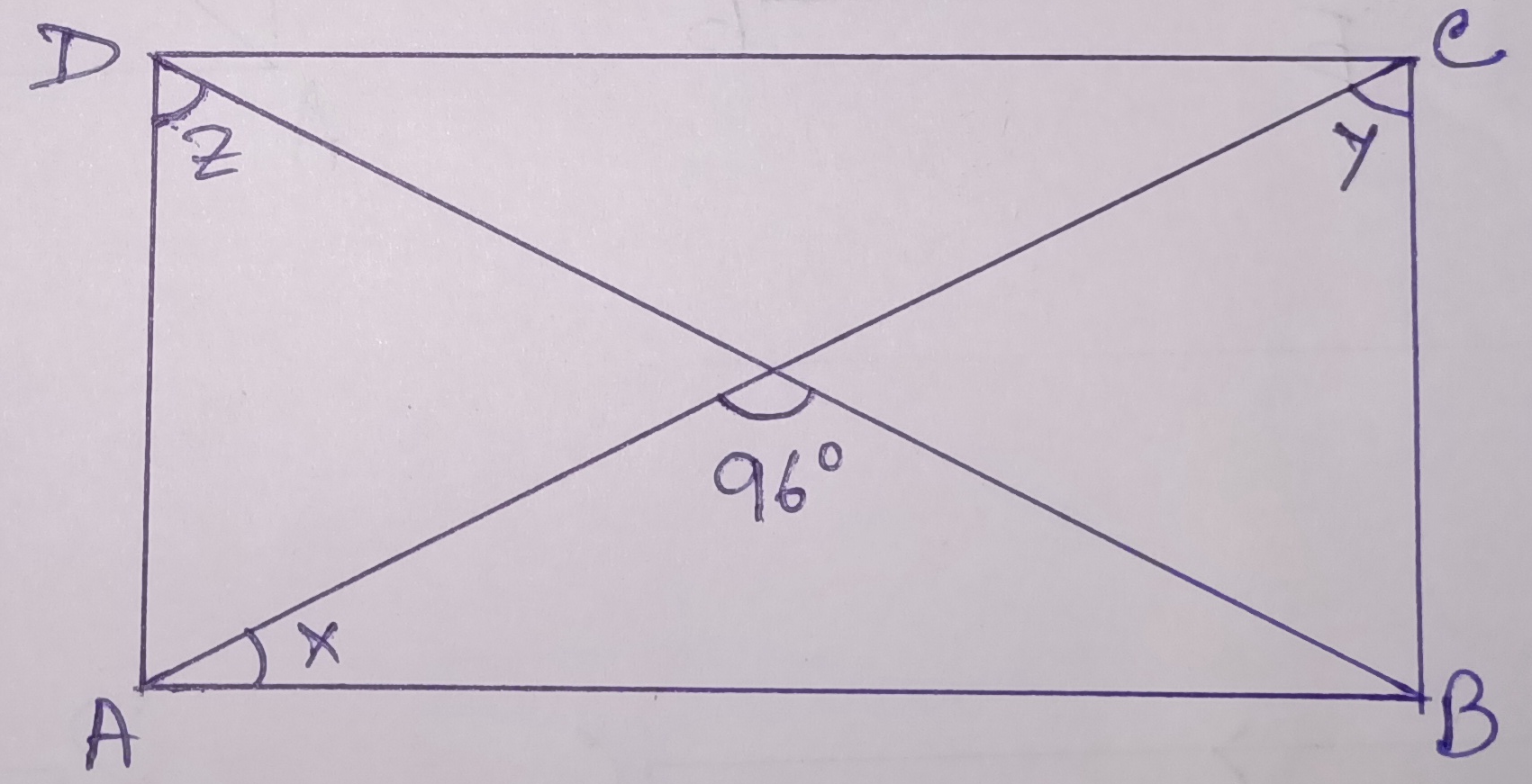
OA = OB = OC = OD
In, ∆ OAB, OA = OB => ∠OBA = ∠OAB = x
The sum of the angles of ∆ OAB = 180⁰
=> x + x + 96⁰ = 180⁰
=> 2x = 180⁰ - 96⁰ = 84⁰
=> x = 42⁰
So, ∠OBA = 42⁰ but ∠ABC = 90⁰
=> ∠OBC = ∠ABC - ∠OBA = 90⁰ - 42⁰ = 48⁰
But, OB = OC
=> ∠OBC = ∠OCB = y
=> y = 48⁰
Again, ∠OAD = ∠DAB - ∠OAB = 90⁰ - x = 90⁰ - 42⁰ = 48⁰
In, ∆ OAD, OA = OD
=> ∠ODA = ∠OAD
=> z = 48⁰
Hence the result is x = 42⁰, y = 48⁰, & z = 48⁰ (Ans.)
Example.3) In the adjoining figure, ABCD is a square. Find x
Ans.) the diagonal BD of the square ABCD bisects ∠ABC
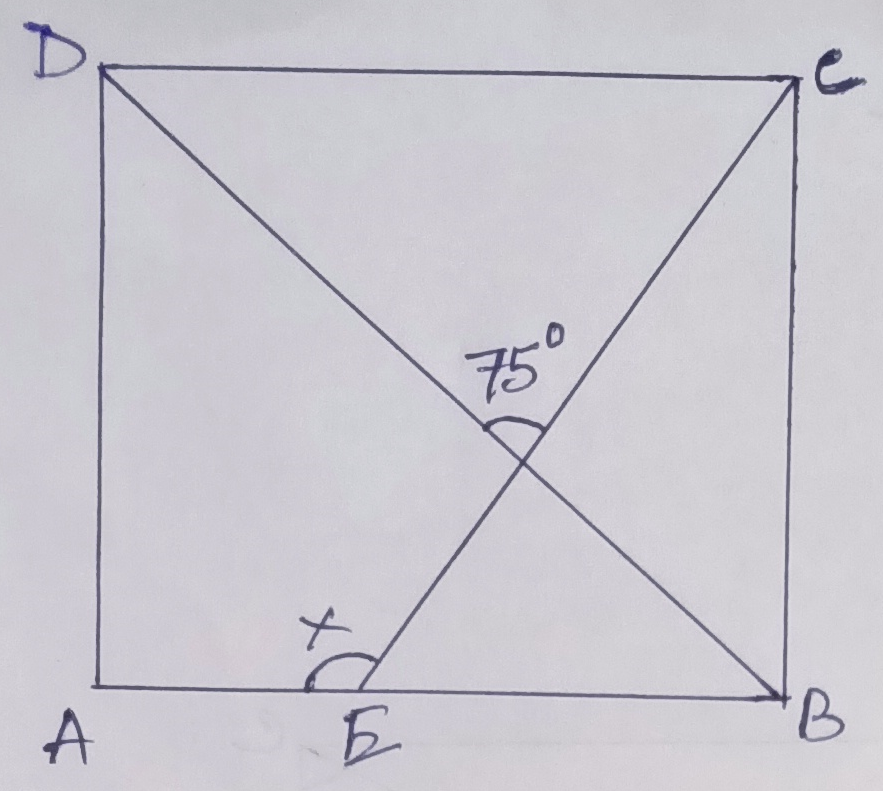
So, ∠PBE = ½ ∠ABC
= ½ X 90⁰ = 45⁰
Also, ∠BPE = opposite ∠DPC = 75⁰
In ∆ PEB, exterior ∠AEP
= ∠BPE + ∠PBE
So, x = 75⁰ + 45⁰ = 120⁰
Hence x = 120⁰ (Ans.)
Example.4) In the adjoining figure, ABCD is a rhombus and ∠BCD = 80⁰, find x & y
Ans.) ABCD is a rhombus, so AC bisects ∠BCD
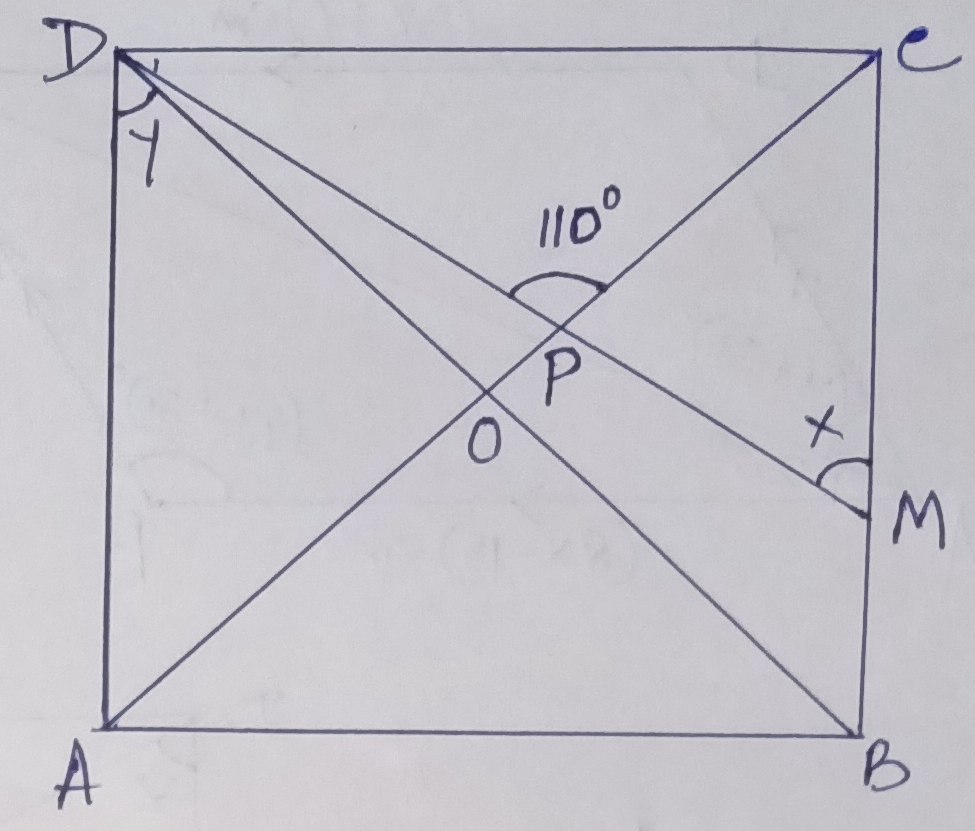
So, ∠PCM = ½ ∠BCD
= ½ X 80⁰ = 45⁰
In, ∆ PCM, exterior ∠DPC
= x + ∠PCM
=> 110⁰ = x + 40⁰
=> x = 110⁰ – 40⁰ = 70⁰
Now, AD || BC (ABCD being rhombus)
=> ∠BCD + ∠ADC = 180⁰
=> 80⁰ + ∠ADC = 180⁰
=> ∠ADC = 180⁰ - 80⁰ = 100⁰
ABCD being a rhombus, the diagonal BD bisects ∠ADC
=> ∠ADB = ½ X ∠ADC
=> y = ½ X 100⁰ = 50⁰
Hence the required result is x = 70⁰, y = 50⁰ (Ans.)
Example.5) In the adjoin figure, the bisectors of the two consecutive angles ∠A & ∠B of the parallelogram ABCD meet at point P. Prove that ∠APB = 90⁰
Ans.) PA & PB are the bisectors of the ∠A & ∠B respectively
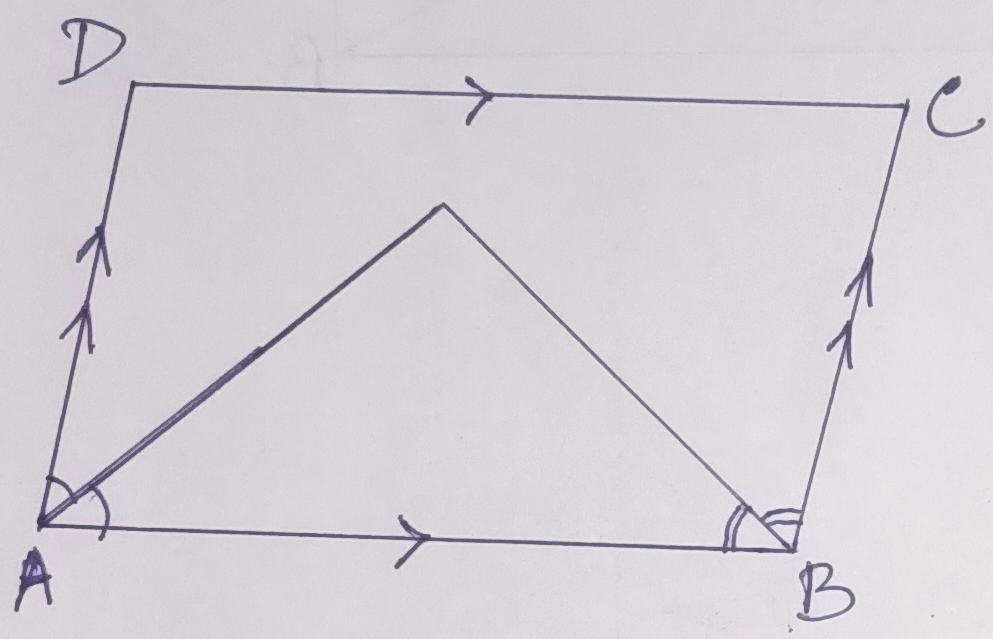
1 1
So, ∠PAB = --------- ∠A and ∠PBA = --------- ∠B
2 2
1
Now, AD || BC => ∠A + ∠B = 180⁰ => -------- (∠A + ∠B) = 90⁰
2
1 1
=> -------- ∠A + --------- ∠B = 90⁰
2 2
=> ∠PAB + ∠PBA = 90⁰
In, ∆ PAB, the sum of angles = 180⁰
=> ∠PAB + ∠PBA + ∠APB = 180⁰
=> 90⁰ + ∠APB = 180⁰
=> ∠APB = 180⁰ - 90⁰ = 90⁰
Hence, ∠APB = 90⁰ (Proved)
Example.6) In the adjoining figure, ABCD is a parallelogram. Prove that a) ∆ ADN ≅ ∆ CBP, and b) AN = CP
Ans.) In, ∆ ADN and ∆ CBP, ∠AND = ∠CPB (= 90⁰),
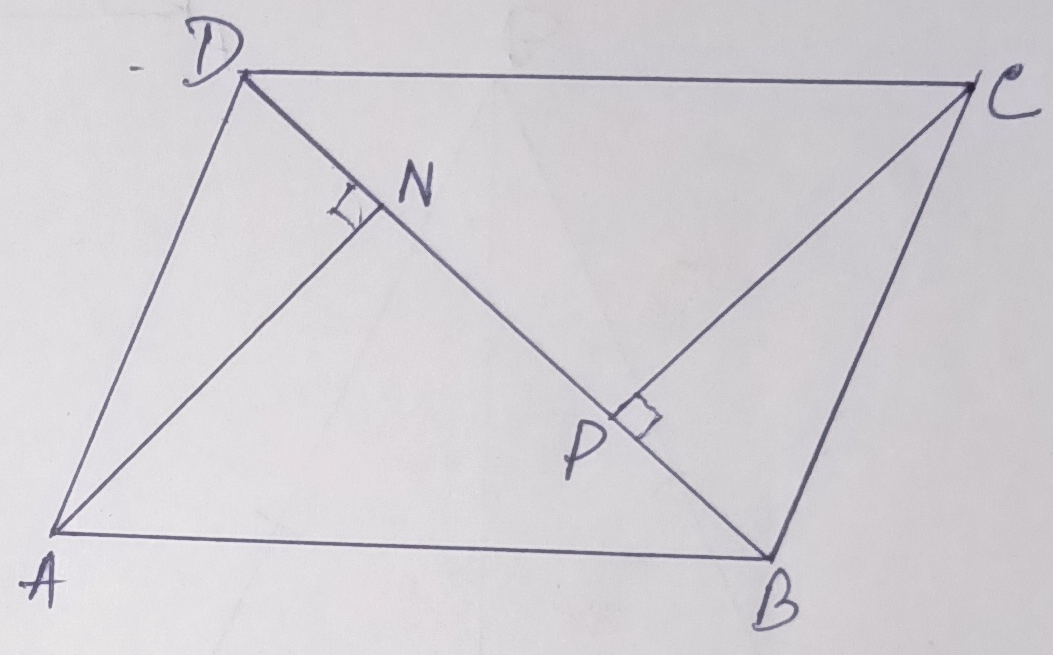
∠ADN = alternate ∠CBP ( AD || BC )
And, AD = BC (opposite sides of a parallelogram)
∆ ADN ≅ ∆ CBP (A-A-S condition of congruence)
So, the corresponding sides are equal.
Hence, AN = CP (Proved)