CLASS-8
THEOREM OF PARALLELOGRAM

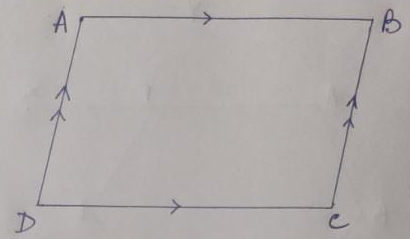
A quadrilateral will be considered as a parallelogram when its opposite sides are parallel. In the figure, ABCD is a parallelogram, in which DC is parallel to AB & DA is parallel to CB. A parallelogram has some special properties which we learn –

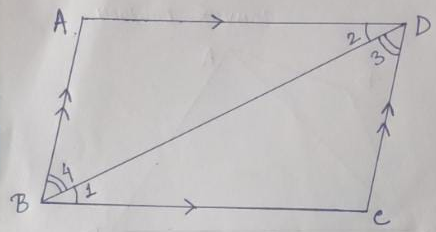
Given – ABCD is a parallelogram in which BC || AD and BA || CD .

To Prove – 1)  BC = AD and BA = CD

2) ∠A = ∠C and ∠B = ∠D

                    3) ∆ BCD ≅  ∆ DAB  and  ∆ BCA ≅ ∆ DAC

Construction – Join the point B & D

Proof -  in ∆ BCD and  ∆ DAB

              ∠1 = ∠2     (BC || AD, alternate angles are equal),

               BD =  BD    (Common)

       And,  ∠3 = ∠4      (BA || CD, alternate angles are equal),

So,  ∆ BCD ≅  ∆ DAB    (A-S-A condition of congruency),

So, the corresponding parts of the triangles are equal

So, BC = AD and  BA = CD             (Proved)

Also,  ∠A = ∠C

We have, ∠1 = ∠ 2  and  ∠4 = ∠3

So,   ∠1 + ∠ 4  = ∠2  +  ∠3

=>    ∠B = ∠D

So,  ∠A = ∠ C  and  ∠B = ∠ D   (proved)

Now,  ∆ BCD ≅  ∆ DAB  (Proved already),

Similarly, ∆ BCA ≅  ∆ DAC

Hence, each diagonal bisects the parallelogram into two congruent parts.  (proved)

Theorem.2)  The diagonals of a parallelogram bisect each other.

Given - ABCD is a parallelogram in which AB || DC, AD || BC and the diagonals AC & BD intersect at the point O.

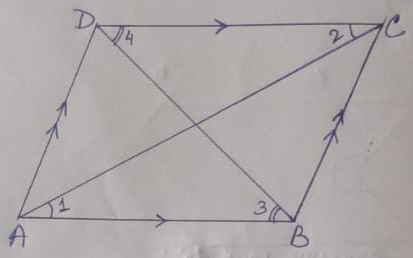
To prove – OA = OC, and OB = OD

Proof - ∆ OAB and ∆ OCD

∠OAB = ∠OCD  (AB || DC and alternate angles are equal)

                         AB = DC   (Opposite sides of a parallelogram are equal)

 And, ∠OBA = ∠ODC   (AB || DC and alternate angles are equal)

       ∆ OAB ≅  ∆ OCD  (A-S-A condition of congruency)

So, the corresponding sides of ∆ OAB and ∆ OCD are equal

So, OA = OC and OB = OD           (proved)

Theorem.3)   If a pair of opposite sides of a quadrilateral are equal and parallel, the quadrilateral is a parallelogram.

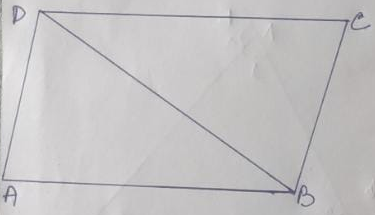
Ans.) Given – ABCD is a quadrilateral in which AB = DC and AB || DC.

To prove – ABCD is a parallelogram

Construction – Join the point B & D

Proof – In ∆ ABD and ∆ CDB,

       AB = DC  (Given)

      ∠ABD = ∠CDB   (AB || DC and alternate angles are equal)

             BD = DB  (common side)

           ∆ ABD ≅ ∆ CDB   (S-A-S condition of congruency)

So, it can be concluded the corresponding parts of these triangles are equal

So, ∠ADB = ∠CBD, but these are alternate angles, so AD || BC.

 Thus, AB || DC and  AD || BC.

Hence, ABCD is a parallelogram.