CLASS-8
GEOMETRY - TYPES OF ANGLES
TYPES OF ANGLES -
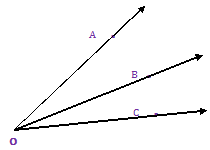
Adjacent Angles –
Two angles are called adjacent angles if they have the same vertex and a common arm and their other arms are on either side of the common arm. In the figure ∠COB and ∠BOA are adjacent angles. While ∠COA and ∠COB are not adjacent angles.
Linear Pair –
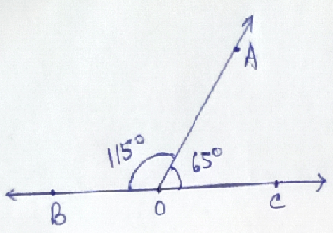
Two adjacent angles are said to form a linear pair if the sum of their measures is 180⁰. Here ∠AOB & ∠AOC form a linear pair because 115⁰ + 65⁰ = 180⁰
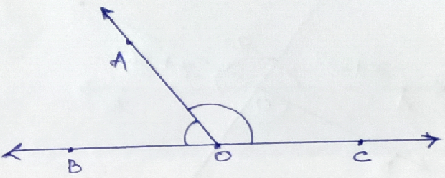
Property - If a ray OA stands on a line BC then the adjacent angles ∠AOB & ∠AOC form a linear pair, that is -
∠AOB + ∠AOC = 180⁰
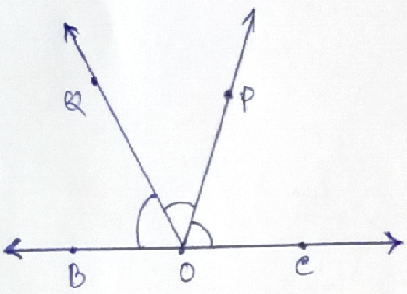
Also, the sum of all the angles at a point of a line on one side of it is 180⁰. Here ∠BOQ + ∠QOP + ∠POC = 180⁰
Complementary Angles –
Two angles are called complementary angles if the sum of their measures is 90⁰, each angle is said to be the complement of the other. For example, two angles of measures 32⁰ and 58⁰ are complementary angles.
Supplementary Angles –
Two angles are called supplementary angles if the sum of their measures is 180⁰, each angle is said to be the supplement of the other. For example, angles of measures 104⁰ and 76⁰ are supplementary angles.
Angles at a Point –
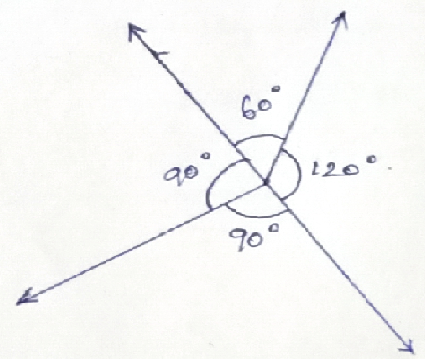
The sum of all the angles at a point, making a complete rotation,
is 360⁰. In the figure, 60⁰ + 90⁰ + 90⁰ + 120⁰ = 360⁰
Vertically Opposite Angles -
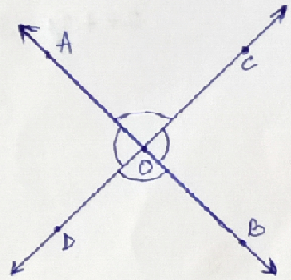
When two straight lines AB
& CD intersect at the point 0 then the pairs (1) ∠AOD
and ∠COB
and (2) ∠AOC and ∠BOD
are called vertically
opposite angles.
Property - If two lines intersect then the vertically opposite angles so formed are equal.
In the figure, ∠AOD = ∠COB
and ∠AOC
= ∠BOD