CLASS-8
VOLUME & SURFACE AREA OF CUBOID
CUBOID –
A cuboid is a solid figure bounded by six rectangular faces and is three-dimensional. The adjacent faces are mutually perpendicular and the opposite faces have the same dimension. A cuboid has eight vertices (M, N, O, P, Q, R, S, T) and twelve edges (MN, OP, PM, ON, QR, RS, ST, TQ, MQ, PT, NR, OS). The volume of a cuboid is considered the product of its length, breadth, and height. We would like denoting the volume = V, length = l, breadth = b, and height = h. we have the formula such as -
volume (V) = length (l) X breadth (b) X height (h)
So, V = l X b X h
V V V
So, l = ---------- , b = ---------- , h = -----------
b X h l X h b X l
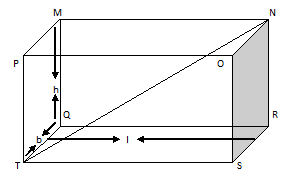
The surface area of a cuboid is considered as the sum of the surface areas of its six rectangular faces, which works out to the following.
As we all know that, area (A) of a rectangle = length (l) X breadth (b) and also know that, every side of a cuboid is a rectangle and the area of a rectangle of every two opposite sides of a cuboid is the same.
So, POST = MNRQ = h X l
PMQT = ONRS = b X h
MNOP = QRST = l X b
Now, the surface area of the cuboid
= POST + MNRQ + PMQT + ONRS + MNOP + QRST
= hl + hl + bh + bh + lb + lb
= 2(hl + bh + lb)
The lateral surface area or the area of the four walls of a cuboid works out to.
The area of the four walls = perimeter of the floor X height
= 2(l + b) X h
Example) The dimensions of a cuboid are 10 cm by 8 cm by 9 cm. find (1) its volume, (2) it's surface area, (3) the surface area of the four walls.
Ans.) Here, l = 10 cm, b = 8 cm, h = 9 cm
(1) the volume of the cuboid = l X b X h
= 10 cm X 8 cm X 9 cm = 720 cmᶟ (Ans.)
(2) its surface area = 2 (lb + bh + hl)
= 2 {(10 X 8) + (8 X 9) + (9 X 10)}
= 2 (80 + 72 + 90)
= 2 X 242 = 484 cm² (Ans.)
(3) Surface area of the four walls = 2 (l + b) X h
= 2 (10 + 8) X 9
= (2 X 18) X 9
= 36 X 9 = 324 cm² (Ans.)