CLASS-8
GEOGRAPHICAL REPRESENTATION OF LINEAR EQUATION & INEQUATION

Geographical Representation –

The solution set of an inequation can be graphically represented on the number line

Example.1) Represent the solution set of the inequation x ≤ 4, x Є N on the number line

Ans.) The solution set for the inequation = { 1, 2, 3, 4 }, which can be represented on the number line by making thick dots or thick small vertical line to represent the numbers 1, 2, 3, & 4

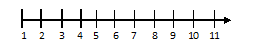
Example.2) Represent the solution set of x ≥ 6, x Є W on the number line

Ans.) The solution set for the inequation x ≥ 6, x Є W is { 6, 7, 8, ……… }. This can be represented on the number line as follows.

The three thick dots or three thick vertical line above the number line indicate that all other subsequent integers are included in the solution set.

Example.3) Represent the solution set of x > 4, x Є R on the number line.

Ans.) The solution set of the given inequation may be represented as follows

The closed circle at 4 indicates that 4 is included in the solution set.

Example.4) Represent the solution set of -3 ≤ x < 6,  x Є R graphically.

Ans.)  The solution set of the inequation -3 ≤ x < 6,  x Є R can be graphically represented by a dark line between -3 and 6 on the number line.

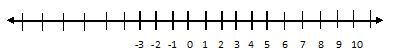
The closed circle at -3 indicates that -3 is included in the solution set. The open circle at 6 indicates that 6 is not included in the solution set.

Example.5)  If the replacement set = { 0, 1, 2, 3, 4, 5, 6, 7, 8 }, find the solution set of each of the following inequalities.

1)  x + 6 < 12,     2)  2x – 3 ≥  10,     3)   4x + 5 ≤  15 + 2x ,        4)  3x – 8 ≥  - 2x + 7

Ans.)  1)  Given, x + 6 < 12   or  x <  6

The replacement set = { 0, 1, 2, 3, 4, 5, 6, 7, 8 }, so the possible values of ‘x’ from the replacement set are 0, 1, 2, 3, 4, & 5

So, the solution set = { 0, 1, 2, 3, 4, 5 }         (Ans.)

2) Given, 2x – 3 ≥  10  or  2x ≥ 13  or  x  ≥ 13/2  or  x  ≥  6.5

But x Є { 0, 1, 2, 3, 4, 5, 6, 7, 8 }. So , x = 7, 8

So, the solution set = { 7, 8 }              (Ans.)

3)  Given 4x + 5 ≤  15 + 2x  or  2x  ≤  10  or  x  ≤  5 

But x Є { 0, 1, 2, 3, 4, 5, 6, 7, 8 }.

So, x = 0, 1, 2, 3, 4, 5

So, the solution set = { 0, 1, 2, 3, 4, 5 }      (Ans.)

4)  Given 3x – 8 ≥  - 2x + 7  or  5x  ≥ 15  or  x ≥ 3

But,  x Є { 0, 1, 2, 3, 4, 5, 6, 7, 8 }. So , x = 3, 4, 5, 6, 7, 8

So, the solution set = { 3, 4, 5, 6, 7, 8 }          (Ans.)

Example.6) Solve 4 (x – 1) < 2x + 6, x Є W and represent the solution set on the number line.

Ans.)  Given,  4 (x – 1) < 2x + 6 

            or,  2x < 10 

            or,   x < 5

Since x Є W, the solution set = { 0, 1, 2, 3, 4 }

The solution set of the given inequation may be represented on the number line as follows. 

Example.7)  If the replacement set is the set of positive integers, find the truth set of the inequation 1 – 2(x – 8) > 4 + x

Ans.)  Given  1 – 2(x – 8) >  x – 4 

       or,  1 – 2x + 16 >  x – 4 

       or,   21 > 3x   

       or,    x < 7

Since the replacement set is the set of positive integers, the solution set =  { 1, 2, 3, 4, 5, 6 }              (Ans.)

Example.8) Find the solution set of the inequation 4(5x – 11) ≤ 31x, given that x is a negative integer.

Ans.)   Given 4(5x – 11) ≤ 31x 

or   20x – 44 ≤  31x   

or   - 11x  ≤  44

        - 11x           44

Or, ---------- ≤ ---------  

        - 11           - 11

 (on dividing by – ve quantity, symbol is reversed)

Or,   x  ≥ - 4

As per the given condition, replacement set should be the set of negative integers,

So, the solution set = { -4, -3, -2, -1 }          (Ans.)

Example.9)  Find solution of 2/3(5x – 9) + 4 ≤ 5 + 4/5(5x – 10),  x Є N

                      2                            4    

Ans.)    Given  --------- (5x – 9) + 4 ≤ --------- (5x – 10)

                      3                            5

             2(5x – 9) + 12          4(5x – 10)

Or,    ------------------ ≤ --------------

                   3                       5

By cross multiplication, we get –

Or,   5 (10x – 18 + 12) ≤  3 (20x – 40)

Or,   5 (10x – 6) ≤  3 (20x – 40)

Or,   50x – 30  ≤  60x – 120

Or,   50x – 60x  ≤  30 – 120

Or,   - 10x ≤ - 90

Or,      x  ≤  9

As per the given condition x Є N, so the solution set = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }                   (Ans.)

Example.10) If the replacement set = { 14, 15, 16, 17, 18, 19, 20 } then find the solution set of 7 + x/5 > 2x/3 – 5

                         x                2x

Ans.) Given,  7 + ---------- > ----------- - 5

                         3                2

            21 + x             2x – 10

Or,   ------------- > -------------

               3                   2

By, cross multiplication –

Or,   2 (21 + x)  >  3 (2x – 10)

Or,     42 + 2x  >  6x – 30

Or,   - 6x + 2x >  - 42 – 30

Or,     - 4x > - 72

Or,     4x  >  72

Or,       x  >  18

Here the replacement set is =  { 14, 15, 16, 17, 18, 19, 20 }

So, the solution set is = { 19, 20 }        (Ans.)

Example.11) Solve the inequality - 3 < 5 – 2x ≤ 1 and represent the solution graphically.

Ans.)  Given  - 3 < 5 – 2x ≤ 1

Or,     - 3 – 5 < 5 – 2x – 5  ≤ 1 – 5       (subtract each side by – 5)

Or,     - 8 < - 2x   ≤  - 4

           - 8            - 2x            - 4

Or,   ---------- < ---------- ≤ ----------

           - 2            - 2             - 2

Or,         4  >  x  ≥  2

So, the solution set is the set of real numbers less than 4 and greater than or equal to 2, which can be represented as shown below –

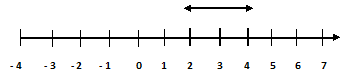
The closed circle at x = 2 indicates that 2 is included in the solution set. The open circle at 4 indicates that 4 is not included in the solution set. (Ans.)