CLASS-8
RELATION & MAPPING - DOMAIN & RANGE

Domain & Range –

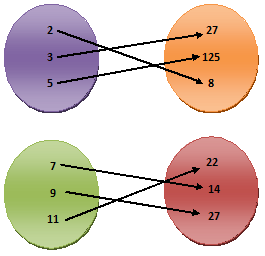
The set of all the first elements (or components) of the ordered pairs of a relation is considered to be the domain of the relation. The set of all the second elements (or components) of the ordered pairs of a relation is to be considered the range of the relation. In the preceding two examples the domains are {2, 3, 5} and {7, 9, 11}, while the ranges are {8, 27, 125} and {14, 22, 27} respectively. Notice that in the first case, domain = set A and range = set B, but in the second case, domain ≠ set A and range ≠ set B. In fact, domain ⊂ set A and range ⊂ set B.

Example.) Let A = {0, 1, 2, 3, 4, 5}, B = {1, 2, 3, 5, 7, 9} and  R = {{(a, b) : a Є A, b Є B and a + b = 8}

1)  Find R and represent it by an arrow diagram,

2)  Find the domain and range of R

Ans.)

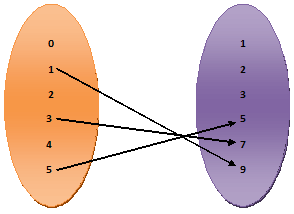
As per the given condition,  R = {(a, b) : a Є A, b Є B and a + b = 10},

Clearly,   1 + 9 = 10, 5 + 5 = 10,  3 + 7 = 10

So, (1, 9) Є R, (5, 5) Є 10,  and (3, 7) Є 10

1)   R = {(1, 9), (5, 5),  and (3, 7)}

The arrow diagram for R is shown alongside …………………………………………(1)     (Ans.)

2) The domain of R = {1, 3, 5}, and the range of R = {5, 7, 9}….…………(2)   (Ans.)