CLASS-8
RELATION & MAPPING - MAPPING

                                               MAPPING

Let, A & B be two non-empty sets, Then a relation which associates each member of A with exactly one member of B is called a Mapping from set A to set B. The unique element b of B that is linked to an element a of set A is called the image of a in B. A mapping is also known as a function.  

Let A = {1, 2, 3, 4, 5} and  B = {a, b, c, d, e}. Consider the following relations from set A to set B

1)  R = {(1, a), (2, c), (3, b), (4, d), (5, e)}

2)  R = {(1, a), (3, d), (3, e), (4, c), (5, c)}

3)  R = {(1, a), (2, a), (3, b), (3, c), (4, c), (5, d), (5, e)}

4)  R = {(1, b), (2, b), (2, c), (3, d), (4, d), (5, e)}

5)  R = {(1, a), (2, b), (3, c), (4, d), (5, e)}

1)  R = {(1, a), (2, c), (3, b), (4, d), (5, e)}

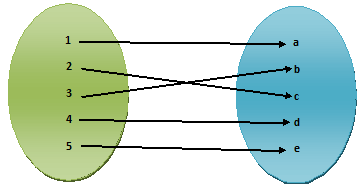
In (1) each member of set A is associated with only one member of B, so, relation (1) is a mapping of function.

2)  R = {(1, a), (3, d), (3, e), (4, c), (5, c)}

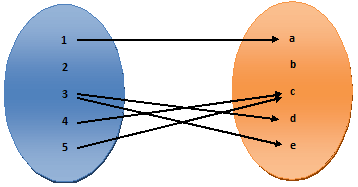
In(2) the member ‘2’ of set A is not associated with any member of set B. so, relation (2) is not a mapping of function.

3)  R = {(1, a), (2, a), (3, b), (3, c), (4, c), (5, d), (5, e)}

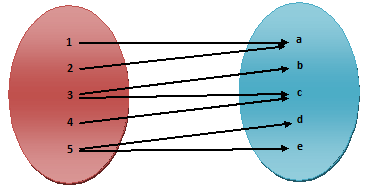
In (3) each member of set A is associated with member of set B. Thus even through two members of set A, 1 and 2 are associated with the same member of set B. The single member 3 of set A, is associated with two members b & c of set B. The two members 3 & 4 of set A, are associated with the same member ‘c’ of set B. The single member 5 of set A is associated with two members d & e of set B, the relation (3) is not a mapping or function

4)  R = {(1, b), (2, b), (2, c), (3, d), (4, d), (5, e)}

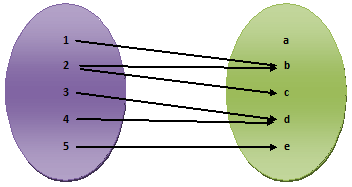
In (4) each member of set A is associated with member of set B. Thus, even through two members 1 & 2 of set A, are associated with the member b of set B. the member 2 of set A is associated with two members b & c of set B. The two members 3 & 4 of set A are associated with member d of set B. the member 5 of set A is associated with member e of set B, but no member of set A is associated with the member a of set B. The relation (4) is not a mapping or function.

5)  R = {(1, a), (2, b), (3, c), (4, d), (5, e)}

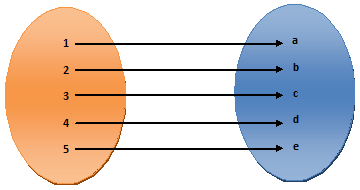
In (5) each member of set A is associated with each member of set B. here each and every single member of set A associated with each and every single member of set B. The relation (5) is a mapping or function.