CLASS-8
RELATION & MAPPING - REPRESENT 'R' IN THE FORM OF ARROW DIAGRAM & ROSTER FORM

RELATION & MAPPING - REPRESENT 'R' IN THE FORM OF ARROW DIAGRAM & ROSTER FORM

Example.1)  Let, A = {3, 4, 5, 6}, B = {27, 64, 125, 216} and R be the relation “is the cube root of” from the set A to set B. Represent R in the form of a arrow diagram and in the roster form.

 Ans.) Since, 27 =   ³√3,  64 = ³√4,  125 = ³√5 , 216 = ³√6, from here we can write 3 R 27, 4 R 64, 5 R 125, 6 R 216.

So, the ordered pairs are (3, 27), (4, 64), (5, 125), and (6, 216). The arrow diagram is shown alongside.

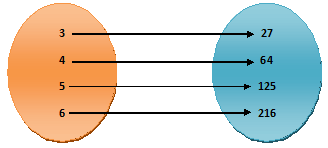
In the roster form, R can be written as follows –

 R = {(3, 27), (4, 64), (5, 125), (6, 216)}

So, R =  {(a, b) : a Є A, b Є B and a = ³√b}

Example.2)  Let, A = {2, 5, 7, 9}, B = {27, 6, 15, 49} and R be the relation “is a factor of” from A to set B. Represent R with the help of an arrow diagram and in the roster form.

Ans.)  2 is a factor of 6,  5 is a factor of 15,  7 is a factor of 49,  9 is a factor of 27

So, we express the relation like – 2 R 6, 5 R 15, 7 R 49, and 9 R 27

So, the ordered pairs are (2, 6), (5, 15), (7, 49), and (9, 27)

So, The arrow diagram is shown below –

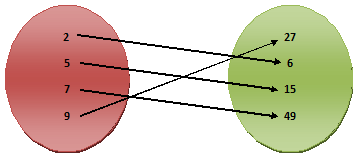
In the Roster form, R can be written as follows –

    R = {(2, 6), (5, 15), (7, 49), (9, 27)}

    R =  {(a, b) : a Є A, b Є B and a is the factor of b}