CLASS-9
AREA OF A QUADRILATERAL WHERE DIAGONALS INTERSECTS AT RIGHT ANGLES
AREA OF A QUADRILATERAL WHERE DIAGONALS INTERSECTS AT RIGHT ANGLES -
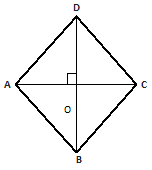
When diagonals of a quadrilateral interest intersect at right angles.
Let the diagonals AC & BD of quad ABCD intersect at O at right angle.
Then area of quad ABCD =
= Area (△ABC) + Area (△ACD)
1 1
= (------ X AC X BO) + (------ X AC X OD)
2 2
1
= ------- X AC X (BO + OD)
2
1
= ------- X AC X BD
2
1
= ------- X (Product of the Diagonals)
2
Example.) Find the area of the quadrilateral whose sides are 10 m, 50 m, 30 m, and 25 m respectively and the angle between first two sides is a right angle.
Ans.) Let ABCD be the given quadrilateral in which AB = 10 m, BC = 50 m, CD = 25 m, DA = 20 m, and ∠ABC = 90⁰
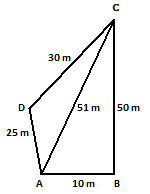
By Pythagoras theorem, we have –
AC = √AB² + BC²
= √10² + 50² = √100 + 2500
= √2600 = 50.99 = 51 m
1
Area of △ABC = ------- X AB X BC
2
1
= ------- X 10 X 50 m² = 250 m²
2
So, In △ACD,
AC = a = 51 m
CD = b = 30 m, and
DA = c = 25 m
1 1
Then, s = ------- (a + b + c) = ------- (51 + 30 + 25)
2 2
106
= ------- = 53 m
2
So, now => (s – a) = (53 – 51) = 2 m
(s – b) = (53 – 30) = 23 m
(s – c) = (53 – 25) = 28 m
So, the area △ACD = √s(s – a) (s – b) (s – c)
= √53 X 2 X 23 X 28 m²
= √68264 m² = 261.27 m² = 261 m²
So, the area of ABCD = Area (△ABC) + Area (△ACD)
= (250 + 261) m²= 511 m²
so, the area of quadrilateral is 511 m² (Ans.)