CLASS-9
AREA OF A TRIANGLE - HERON's FORMULAE

          1

S =  -------- (a + b + c) is called semi-perimeter of the triangle.

          2

Then, Area of the triangle = √s(s – a)(s – b)(s – c) sq.units

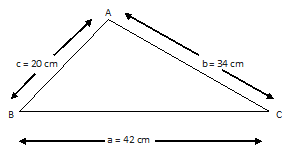
Example.1)  Find the area of a triangle whose sides are 42 cm, 34 cm, and 20 cm. hence find the height corresponding to the longest side.

Ans.) As per the given condition, let a = 42 cm, b = 34 cm, and c = 20 cm.

                  1                        1

          s = ------- (a + b + c) = ------- (42 + 34 + 20)

                  2                        2

                                           96

                                      = ------- =  48 cm

                                            2

So,  (s – a) = 48 – 42 = 6 cm

      (s – b) = 48 – 34 = 14 cm

      (s – c) = 48 – 20 = 28 cm

Now, Area of the Triangle = √s(s – a)(s – b)(s – c)

                              =  √48 X 6 X 14 X 28

                              =  336 cm²

Length of the longest side = 42 cm

Let the corresponding height be y cm.

                    1

Then, Area = (------- X 42 X y) cm² =  21 y cm²

                    2

As per the condition, 21 y cm² = 336 cm²

                                 y = 16

Hence, the height corresponding to the longest side is 16 cm.   (Ans.)