CLASS-9
AREA, PERIMETER, AND DIAGONAL OF RECTANGLE

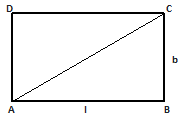
For a Rectangle with Length = l units and Breadth = b units, we have

a)  Perimeter = 2 (Length + Breadth) = 2 (l + b) units                     

b)  Area = (Length X Breadth) = (l X b) sq. units

c)   Diagonal = √l² + b²  units   

Example.1) The length of a rectangular plot is twice its breadth. If the perimeter of the plot is 360 m, find its area.

Ans.)   Let the breadth of the plot is ‘x’ meters

Then, as per the given condition its length would be = 2x

As per the rules –

Perimeter = 2 X (Length + Breadth)

                   = 2 X (2x + x)

                   = 2 X 3x = 6x

So,       6x = 360

           x = 60

so, breadth of the plot is 60 m, and

the length of the plot is 60m X 2 = 120 m

Hence, the area of the plot is = (length X breadth)

                                  =  (60 m X 120 m)

                                  = 7200 m²

the area of the plot is  7200 m²   (Ans.)

Example.2) Find the area of a rectangular plot of land one of whose sides measures 35 m and the length of whose diagonal is 37 m

Ans.) Let, ABCD be the rectangular plot.

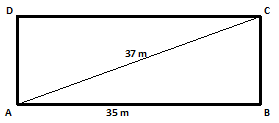
From above rectangle ABCD, AB = 35 m, and AC = 37 m

As per Pythagoras theorem =>  AC² = AB² + BC²

                           Or,    BC² = AC² - AB²

                           Or,    BC = √(AC² - AB²)

                                      = √(37² - 35²)

                                      = √(1369 – 1225)

                                      = √144 = √12² =  12 m

Now, the area of the rectangle is = (35 m X 12 m) = 420 m²  (Ans.)

Example.3) A rectangular table mat has an area of 60 m². If its diagonal and longer side together equal 4 times the shorter side, find the length of the table mat.

Ans.) Let the length of the table mat is x meter and its breadth is y meters.

Then, lengh of the diagonal is = √(x² + y²) m

As per the given condition, area of the table mat => xy = 60 m²………(i)

Also, as per the another given condition

            =>  √(x² + y²) + x = 4y ……………….(ii)

            =>  √(x² + y²) = 4y – x

Now squaring both the side, we get –

        =>   {√(x² + y²)}² = (4y – x)²

        =>   x² + y² = 16y² - 8xy + x²    [(a ± b)² = a² ± 2ab + b²]

        =>    15y² - 8xy = 0 

Substituting the value of (i), we get –

                       =>  15y² = 8 X 60

                       =>  y² = 8 X 4

                       =>  y = √4 X 2 X 4 = 4√2 = 5.65 m

Hence, the length of the table mat =>  xy = 60

                                       =>  5.65 x = 60

                                       =>   x  =  10.62 m 

 So, the length of the table mat is 10.62 m    (Ans.)