CLASS-9
AREA OF A TRIANGLE
AREA OF TRIANGLE –
1
Area of Triangle = ------- X Base X Corresponding Height
2
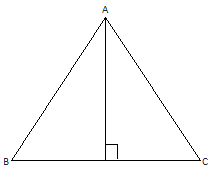
In any triangle △, there are three sides. Any sides of the triangle may be taken as base and the length of perpendicular from the opposite vertex to the base is to considered as a corresponding height.
1
In given figure, area of △ ABC = (------- X BC X AD) sq. units
2
There are some examples are given below –
Example.1) Find the area of a triangle with base 36 cm and height 24 cm
1
Ans.) Area of the given triangle = ------- X Base X Height
2
1
= ------ X 36 X 24
2
= 18 X 24 = 432 cm² (Ans.)
Example.2) The base of a any triangular field is 4 times of its altitude. If the cost of cultivating the field at $ 12 per hector is $ 1536. Find its base & height.
Total Cost
Ans.) Area of the Triangle = ---------------
Rate
1536
= --------- = 128 hectors
12
= (128 X 10000) m² [ where, 1 hector = 10000 m² ]
= 1280000 m²
Let the altitude of the field be z meters, then the base of the triangle would be 4 z (as per the given condition)
1 4z²
So, Area = (------ X 4z X z) m² = (-------) m² = 2 z² m²
2 2
As per the given condition –
2 z² m² = 1280000 m²
Or, z² = 640000
Or, z = √640000 = √800²
Or, z = 800
So, altitude = 800 m, and base = 4 z = 4 X 800
= 3200 m
Hence the required altitude is 800 m & base is 3200 m (Ans.)