CLASS-9
MEAN & MEDIAN - UNGROUPED FREQUENCY DISTRIBUTION - DIRECT METHOD
MEAN & MEDIAN- UNGROUPED FREQUENCY DISTRIBUTION-
DIRECT METHOD-
Let, y₁, y₂, y₃,…………, yₑ of a variable y, occurring with frequencies f₁, f₂, f₃,…………, fₑ respectively.
Then the mean of these given observation is given by –
(f₁y₁ + f₂y₂ +………..+ fₑyₑ) ∑ fᵢ yᵢ
Mean, ӯ = --------------------------- = -----------
(f₁ + f₂ + ……………+ fₑ) ∑ fᵢ
Example.1) The ages of 50 students in a class given below –

Find the mean age of class.
Ans.) As per the given condition, we should prepare the table given below -
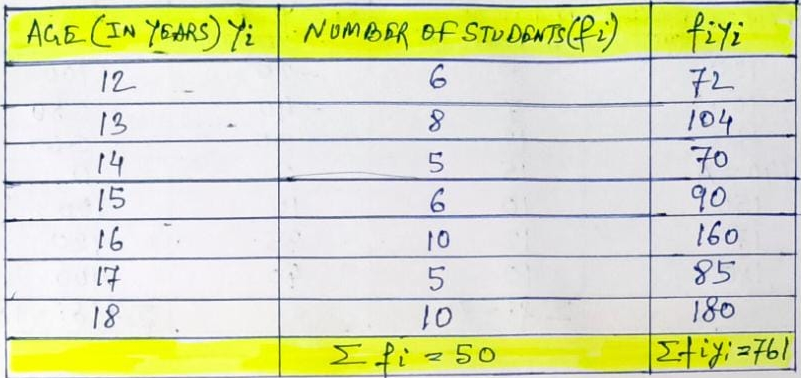
Ʃ fᵢyᵢ 761
So, mean age = --------- = -------- = 15.22 years (Ans.)
Ʃ fᵢ 50
Example.2) If the mean of the following frequency distribution is 24.5. Then find the value of z.

Ans.) We prepare the table as under –
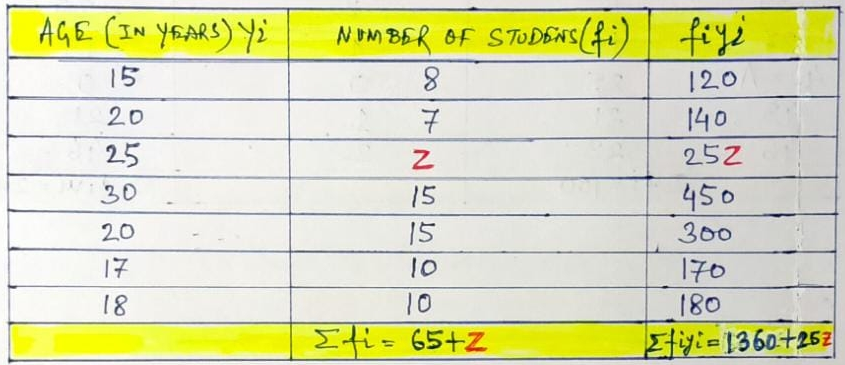
Ʃ fᵢyᵢ
As per the given condition, mean age = ----------- = 22.5
Ʃ fᵢ
1360 + 25 Z
Or, ----------------- = 22.5
65 + Z
Or, 1360 + 25 Z = 22.5 X (65 + Z)
Or, 1360 + 25 Z = 1462.5 + 22.5 Z
Or, 25 Z – 22.5 Z = 1462.5 – 1360
Or, - 2.5 Z = 102.5
Or, Z = 41
Hence the obtained value of Z = 41 (Ans.)
Example.3) The mean of the following distribution is 16.5

Find the missing frequencies of P & Q
Ans.) We prepare the table given below –
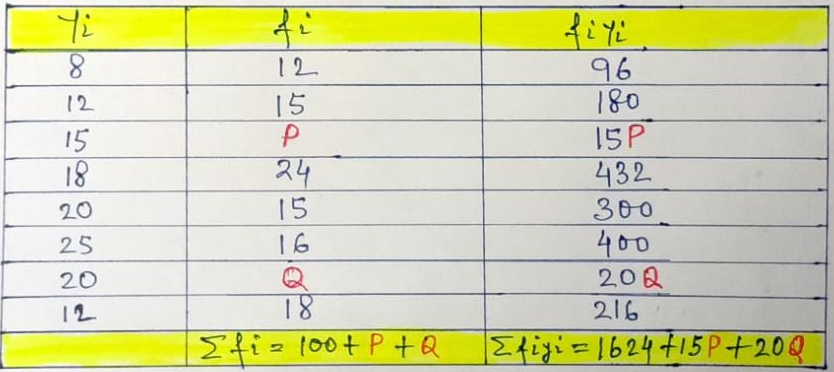
Here, Ʃ fᵢ = 100 + P + Q.
But, Ʃ fᵢ = 180
So, 100 + P + Q = 180
So, P + Q = 80 …………………….(i)
Ʃ fᵢyᵢ 1624 + 15 P + 20 Q
Also, mean = ----------- = ----------------------
Ʃ fᵢ 100 + P + Q
But, as per the given condition the mean is given 16.5
1624 + 15 P + 20 Q
So, ------------------------ = 16.5
100 + P + Q
1624 + 20 P + 20 Q – 5P
So, ---------------------------- = 16.5
100 + P + Q
1624 + 20 (P + Q) – 5P
So, ------------------------- = 16.5
100 + (P + Q)
Now, we will substitute the value of (i), and we get –
1624 + (20 X 80) – 5P
So, ------------------------ = 16.5
100 + 80
So, 1624 + 1600 – 5P = (16.5 X 180)
So, 3224 – 5P = 2970
So, 5P = 3224 – 2970 = 254
So, 5P = 254
So, P = 50.8
Now we will substitute the value of P in (i), and we get –
P + Q = 80
Or, 50.8 + Q = 80
Or, Q = 80 – 50.8 = 29.2
Hence, P = 50.8, and Q = 29.2 (Ans.)