CLASS-9
MEDIAN OF DISCRETE SERIES
Median Of Discrete Series –
Method – First arrange the terms in an ascending or a descending order. Now we will prepare a cumulative frequency table. Let the total frequency be ‘n’
n + 1
i) If n is odd, then median = size of (-------)th item.
2
ii) If n is even, then median =
1 n n
------ {size of (------)th item + size of (------- + 1)th item}
2 2 2
Example.1) The following table gives a description of the marks obtained by 39 students of a class.

Find the median of marks obtained.
Ans.) Arranging the terms in an ascending order, we have –

Now, preparing the cumulative frequency table, we have –
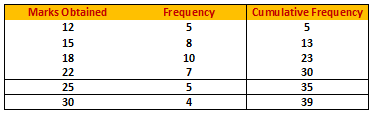
Total number of items = 39, which is odd.
39 + 1
So, median marks = marks obtained by the (---------)th student
2
= marks obtained by the 20th students
But, the above table shows that each one of the students from 19th to 21st gets 18 marks. Thus the 20th student gets 18 marks. Hence the median marks 21. (Ans.)
Example.2) The height (in cm) of the 50 students of a class are given below –

Find the median height.
Ans.) We prepare the cumulative frequency table as given below
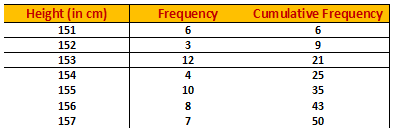
Number of items, n = 50, which is even.
n 50 n 50
So, ------ = ------ = 25 and (----- + 1) = (----- + 1) = 26
2 2 2 2
As per the formulae –
1
Median = ------ [(value of 25th item) + (value of 26th item)]
2
But, the above table shows that the height of the 25th student is 154 cm while that of the 26th student is 155 cm.
1 309
So, the median height = ------ (154 + 155) cm = ------- cm
2 2
= 154.5 cm
Hence the median height is 154.5 cm (Ans.)