CLASS-9
METHOD OF CROSS MULTIPLICATIONS - SIMULTANEOUS LINEAR EQUATIONS

Method of Cross Multiplication (Simultaneous Linear Equations) –

Theorem – consider the system of linear equations

                                                       a₁            b₁

a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, where -------- ≠ --------

                                                       a₂            b₂

   The above system has a unique solution, given by

          (b₁c₂ - b₂c₁)                   (c₁a₂ - c₂a₁)

  x = ---------------, and  y = ----------------

          (a₁b₂ - a₂b₁)                   (a₁b₂ - a₂b₁)

PROOF.)  The given equations are –

          a₁x + b₁y + c₁ = 0 ………………...(i)

          a₂x + b₂y + c₂ = 0 ………………...(ii)

multiplying (i) by b₂, (ii) by b₁ and subtracting, we get –

      (a₁b₂ - a₂b₁) x = (b₁c₂ - b₂c₁)

         (b₁c₂ - b₂c₁)                             

 x = ----------------

         (a₁b₂ - a₂b₁)                            

Multiplying (ii) by a₁, (i) by a₂ and subtracting, we get –

 (a₁b₂ - a₂b₁) y = (c₁a₂ - c₂a₁)

                (c₁a₂ - c₂a₁)

So, y  =  -----------------

                (a₁b₂ - a₂b₁)

Thus the given system of equations has a unique solution given by –

        (b₁c₂ - b₂c₁)                     (c₁a₂ - c₂a₁)

x = ----------------,  and  y = ----------------

        (a₁b₂ - a₂b₁)                     (a₁b₂ - a₂b₁)

Note.– The above result may be written as

           x                       y                      1

  --------------- = ---------------- = ----------------

      (b₁c₂ - b₂c₁)          (c₁a₂ - c₂a₁)           (a₁b₂ - a₂b₁)

Remarks: The diagram given below helps in remembering        

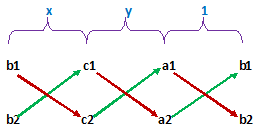
Rule:- Numbers with downward arrows are multiplied first, and from this product, the product of numbers with upward arrows is subtracted.

          x                       y                       1

---------------- = ---------------- = ----------------

   (b₁c₂ - b₂c₁)            (c₁a₂ - c₂a₁)           (a₁b₂ - a₂b₁)