CLASS-9
PERIMETER & AREA OF QUADRILATERAL - PROBLEM & SOLUTION
Example.1) The length and breadth of a rectangular grassy plot are in the ration 7 : 4. A path 4 m wide running all around outside it has an area of 416 m². Find the dimensions of the grassy plot.
Ans.) Let the length & breadth of the grassy plot be 7a and 4a meters respectively. Then the area of the plot is = (7a X 4a) m² = (28 a²) m²
Now, as per the given condition, a path of 4 m wide running all around outside area and it has area of 416 m²
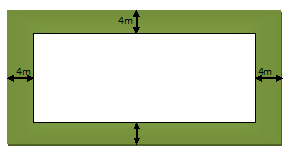
As you can find from the above picture, in length there is = 4 m + 4 m = 8 m more length to be added in given length, and in breadth also there is = 4 m + 4 m = 8 m more breadth is to be added in the given breadth size.
Now, the length along with running area should be = (7a + 8) m
And, the breadth along with running area should be = (4a + 8) m
So, area of the plot including the path = (7a + 8) (4a + 8) m²
Now, area of the path => [{(7a + 8)(4a + 8)} – 28a² ]m² = 416 m²
Or, (28a² + 32a + 56a + 64) – 28a² = 416
Or, 88 a = 416 – 64
Or, 88a = 352
Or, a = 352/88 = 4
So, now the length of the plot is 7a = 7 X 4 = 28 m, and width of the given plot is = 4a = 4 X 4 = 16 m (Ans.)
Example.2) A rectangular lawn 64 m by 48 m has two roads, each 5 m wide , running in the middle of it, one parallel to length and other parallel breadth. Find the cost of graveling them at $ 2.80 per m²
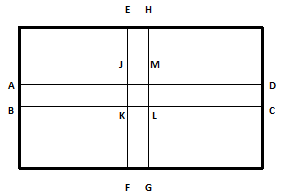
From the above picture, area of road ABCD = (64 X 5) m² = 320 m²
Area of road EFGH = (48 X 5) m² = 240 m²
Clearly, area JKLM is common to both of the above roads.
Area JKLM = (5 X 5) m² = 25 m²
Area of the road to graveled = {(320 + 240) – 25} m² = 535 m²
Cost of graveling of the path = $ (2.80 X 535) = $ 1498 (Ans.)
Example.3) If the length and breadth of a rectangular room are each increased by 1 m, then the area of the floor increased by 21 m². if the length is increased by 1 m and breadth is decreased by 1 m, then the area is decreased by 7 m². Find the perimeter of the floor.
Ans.) Let, the original length and breadth of the room be x and y meters respectively. Then, original area of the floor = (xy) m²
When both length and breadth are increased by 1 m
New length = (x + 1) m
New breadth = (y + 1) m
New area = (x + 1)(y + 1) m²
New area => [{(x + 1) (y + 1)} – xy] = 21
=> xy + y + x + 1 – xy = 21
=> y + x = 21 - 1
=> y + x = 20 ……………………….(i)
When length is increased by 1 m and breadth is decreased by 1 m
New length = (x + 1) m
New breadth = (y - 1) m
New area = (x + 1)(y - 1) m²
New area => [xy - {(x + 1) (y - 1)}] = 7
=> xy – (xy + y - x – 1) = 21
=> x - y + 1 = 7
=> x - y = 6 ……………………….(ii)
Adding (i) & (ii), and we get –
x + y = 20
x – y = 6
-----------------
2x = 26
Or, x = 13
Now, we will substitute the value of x in (i), and we get -
y + x = 20
or, y + 13 = 20
or, y = 7
so, the perimeter of the floor –
[2 (length + Breadth)] = 2 (13 + 7) = 2 X 20
= 40 m (Ans.)