CLASS-9
VOLUME & SURFACE AREA OF SOLIDS - LATERAL SURFACE AREA OF CUBOID
LATERAL SURFACE AREA OF CUBOID -
Cuboid – A rectangular solid bounded by six rectangular plane faces is called a cuboid. A match box, a chalk box, a brick, a block, a book, etc., are all examples of a cuboid. A cuboid has 6 rectangular faces, 12 edges and 8 vertices. Let us considered a cuboid of length = l units, breadth = b units, and height = h units.
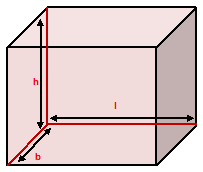
The four faces which meet the base of a cuboid are called the lateral faces of the cuboid. The sum of areas of the four walls of a cuboid is called its lateral surface area.
Lateral surface area of a cuboid = [2 (l + b) X h] sq. units
Thus, Area of four walls of a room = [2 (l + b) X h] sq. units
Example.) Find the volume, the total surface area and the lateral surface area of a rectangular solid 8 m long, 4.5 m broad, and 75 cm high.
Ans.) As per the formulae, volume of the cuboid =
(l X b X h) cubic units
75
Here, h = ------- m [100 cm = 1 m, so 1 cm = 1/100 m]
100
= 0.75 m
l = 8 m, b = 4.5 m
now, according to the formulae -
(l X b X h) cubic unit = (8 X 4.5 X 0.75) m³
= 27 m³ -------------------(i)
As per the formulae, total surface are of the solid
= 2 (lb + bh + lh) sq. units
= 2 {(8 X 4.5) + (4.5 X 0.75) + (8 X 0.75)}
= 2 (36 + 3.375 + 6) m²
= (2 X 45.375) m²
= 90.75 m² ………………………..(ii)
As per the formulae, lateral surface of the solid
= [2(l + b) X h] sq. units
= [2(8 + 4.5) + 0.75] m²
= 25.75 m² ………………………..…(iii)